4.5 Calculating Probabilities Using Pedigree Charts

Once the mode of inheritance of a disease or trait is identified, some inferences about the genotype of individuals in a pedigree can be made, based on their phenotypes and where they appear in the family tree.  Given these genotypes, it is possible to calculate the probability of a particular genotype being inherited in subsequent generations.  This can be useful in genetic counselling, for example when prospective parents wish to know the likelihood of their offspring inheriting a disease for which they have a family history.

Probabilities in pedigrees are calculated using knowledge of Mendelian inheritance and the same basic methods as are used in other fields.

The first formula is the product rule: the joint probability of two independent events is the product of their individual probabilities; this is the probability of one event AND another event occurring.

For example:

The probability of a rolling a “five” with a single throw of a single six-sided die is [latex]\frac{1}{6}[/latex], and the probability of rolling “five” in each of three successive rolls is  [latex]\frac{1}{6}\times\frac{1}{6}\times\frac{1}{6}=\frac{1}{216}[/latex].

The second useful formula is the sum rule, which states that the combined probability of two independent events is the sum of their individual probabilities. This is the probability of one event OR another event occurring.

For example:

The probability of rolling a five or six in a single throw of a dice is [latex]\frac{1}{6}+\frac{1}{6}=\frac{1}{3}[/latex].

With these rules in mind, we can calculate the probability that two carriers (i.e., heterozygotes) of an AR disease will have a child affected with the disease as [latex]\frac{1}{2}\times\frac{1}{2}=\frac{1}{4}[/latex], since for each parent, the probability of any gametes carrying the disease allele is ½.   This is consistent with what we already know from calculating probabilities using a Punnett square (e.g., in a monohybrid cross Aa × Aa, ¼ of the offspring are aa).

We can likewise calculate probabilities in the more complex pedigree shown in Figure 4.5.1.

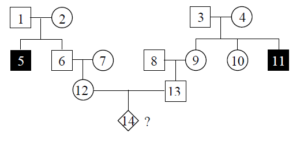
Assuming the disease has an AR pattern of inheritance, what is the probability that individual #14 will be affected? We can assume that individuals #1, #2, #3 and #4 are heterozygotes (Aa), because they each had at least one affected (aa) child, but they are not affected themselves. This means that there is a [latex]\frac{2}{3}[/latex] chance that individual #6 is also Aa. This is because according to Mendelian inheritance, when two heterozygotes mate, there is a 1:2:1 distribution of genotypes AA:Aa:aa. However, because #6 is unaffected, he can’t be aa, so he is either Aa or AA, but the probability of him being Aa is twice as likely as AA.  By the same reasoning, there is likewise a [latex]\frac{2}{3}[/latex] chance that #9 is a heterozygous carrier of the disease allele.

Media Attribution

• Figure 4.5.1 Original attributed to Unknown (2017), CC BY-NC 3.0, Open Genetics Lectures

Reference

Unknown. (2017). Figure 15. Individuals in this pedigree are labeled with…[digital image]. In Locke, J., Harrington, M., Canham, L. and Min Ku Kang (Eds.), Open Genetics Lectures, Fall 2017 (Chapter 23, p. 7). Dataverse/ BCcampus. http://solr.bccampus.ca:8001/bcc/file/7a7b00f9-fb56-4c49-81a9-cfa3ad80e6d8/1/OpenGeneticsLectures_Fall2017.pdf

Long Description

• Figure 4.5.1 Complex pedigree chart showing four generations. The purpose of this chart is simply to demonstrate that we are able to use the rules of probability to calculate the percentage chance of inheritance of a particular trait within a given family tree. The individuals in the chart are labelled from 1 to 14, throughout successive generations. All are shown to be unaffected, except for individual 5, who is part of Generation II and individual 11, also part of generation II. The text directly proceeding this image describes in detail, how this chart can be interpreted using the rules of probability. [Back to Figure 4.5.1]